1
Überschneidenden Bereich zweier Kreise berechnen
Hallo,
hab mal wieder ein kleines Problem, was jetzt eigentlich weniger mit Programmieren zutun hat sondern mehr mit Mathematik.
Und zwar hab ich folgendes:
Ich habe 2 Kreise (später dann maximal 128 Stück), von denen ich die Koordinaten weiß und anhand deren die Überschneidung finden möchte.
So zum Beispiel:
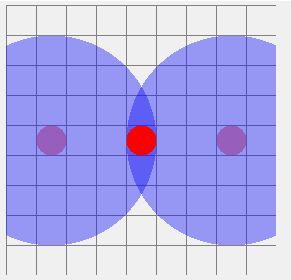(Der mittlere Kreis braucht nicht beachtet zu werden)
Also; es soll nach dem WarDrive-Prinzip funktionieren, bei dem man WLAN-Router lokalisieren kann, zum hineinarbeiten gehe ich mal in der Annahme dass der mittlere Punkt der AP ist und die beiden Punkte links und rechts jeweils ein Standort ist an dem man 100% Empfang hat.
Mal angenommen, 100% Signalstärke reicht für 100 Meter (nur als Beispiel), im Bild mit einem Radius von 3,5 Feldern.
Wie errechne ich anhand von mehreren Datensätzen von Koordinaten und Radius den Punkt an dem sich alle treffen? Beziehungsweise die genaue Mitte falls sie sich mal nicht treffen?
Oder noch schwieriger:
Ich habe eine Liste folgender Daten:
- Koordinaten
- Signalstärke (0-100)
Und ich möchte die Stelle finden, an der die Signalstärke am höchsten ist.
Wäre für letzteres folgender Ansatz richtig (auch wenn er sehr rechenintensiv ist) ?
Wenn ich für die Koordinaten {X=0; Y=0} die Signalstärke 100 hab und davon ausgehe, dass ein solches WLAN maximal 5 Meter entfernt ist, dann könnte ich ja eine Liste von Punkten erstellen, die sich innerhalb dieses Radius befinden. So hätte ich schon mal viele Punkte, an denen das WLAN 100% hat.
Jetzt weiß ich aber noch nicht, ob das WLAN sich in Richtung Norden, Osten, Süden oder Westen befindet.
Bewege ich mich jetzt am äußeren Rand dieses Radius und bekomme noch 50%, dann überschreibe ich diese Punkte in der Liste mit dem Wert 50
Natürlich ist mir bewusst, dass man in der Praxis nicht so oft genau 100% oder genau 50% hat wenn man ein WLAN lokalisieren möchte. Natürlich werde ich eben den Wert loggen den ich gerade finde.
Passt dieser Ansatz?
Seid mir bitte nicht böse, wenn ich sich im Text auf einmal meine Fragestelung ein bisschen verändert hat...
Ich wäre euch sehr dankbar, wenn ihr mir helfen könntet.
Gruß Chris
hab mal wieder ein kleines Problem, was jetzt eigentlich weniger mit Programmieren zutun hat sondern mehr mit Mathematik.
Und zwar hab ich folgendes:
Ich habe 2 Kreise (später dann maximal 128 Stück), von denen ich die Koordinaten weiß und anhand deren die Überschneidung finden möchte.
So zum Beispiel:
Also; es soll nach dem WarDrive-Prinzip funktionieren, bei dem man WLAN-Router lokalisieren kann, zum hineinarbeiten gehe ich mal in der Annahme dass der mittlere Punkt der AP ist und die beiden Punkte links und rechts jeweils ein Standort ist an dem man 100% Empfang hat.
Mal angenommen, 100% Signalstärke reicht für 100 Meter (nur als Beispiel), im Bild mit einem Radius von 3,5 Feldern.
Wie errechne ich anhand von mehreren Datensätzen von Koordinaten und Radius den Punkt an dem sich alle treffen? Beziehungsweise die genaue Mitte falls sie sich mal nicht treffen?
Oder noch schwieriger:
Ich habe eine Liste folgender Daten:
- Koordinaten
- Signalstärke (0-100)
Und ich möchte die Stelle finden, an der die Signalstärke am höchsten ist.
Wäre für letzteres folgender Ansatz richtig (auch wenn er sehr rechenintensiv ist) ?
Wenn ich für die Koordinaten {X=0; Y=0} die Signalstärke 100 hab und davon ausgehe, dass ein solches WLAN maximal 5 Meter entfernt ist, dann könnte ich ja eine Liste von Punkten erstellen, die sich innerhalb dieses Radius befinden. So hätte ich schon mal viele Punkte, an denen das WLAN 100% hat.
Jetzt weiß ich aber noch nicht, ob das WLAN sich in Richtung Norden, Osten, Süden oder Westen befindet.
Bewege ich mich jetzt am äußeren Rand dieses Radius und bekomme noch 50%, dann überschreibe ich diese Punkte in der Liste mit dem Wert 50
Natürlich ist mir bewusst, dass man in der Praxis nicht so oft genau 100% oder genau 50% hat wenn man ein WLAN lokalisieren möchte. Natürlich werde ich eben den Wert loggen den ich gerade finde.
Passt dieser Ansatz?
Seid mir bitte nicht böse, wenn ich sich im Text auf einmal meine Fragestelung ein bisschen verändert hat...
Ich wäre euch sehr dankbar, wenn ihr mir helfen könntet.
Gruß Chris
Auf Facebook teilen
Auf Twitter teilen
Auf Reddit teilen
Auf Linkedin teilenBitte markiere auch die Kommentare, die zur Lösung des Beitrags beigetragen haben
Content-ID: 292339
Url: https://administrator.de/contentid/292339
Ausgedruckt am: 24.11.2024 um 22:11 Uhr
1 Kommentar
Hallo Chris,
mal als Ansatz für Dein erstes Problem, die Lösung für das zweite (schwierigere) solltest Du daraus selbst ableiten können:
Die halbe Distanz zwischen zwei Punkten A und B mit den Koordinaten (Xa|Ya) und (Xb|Yb) lässt sich mit ein wenig Vektoralgebra berechnen. Sie entspricht dem halben Betrag des Richtungsvektors zwischen den Punkten A und B:
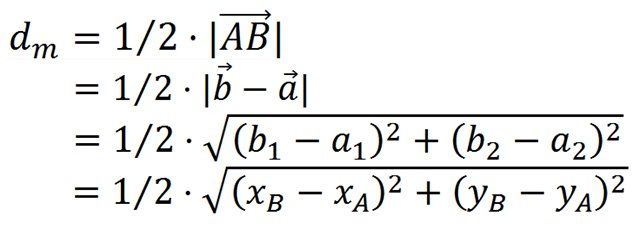
Die Koordinaten der halben Distanz lassen sich nach der Mittelpunktsformel berechnen:
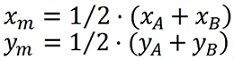
Wenn die halbe Distanz zwischen den WLAN Access Points A und B kleiner als die Reichweite beider Access Points ist, dann überschneiden sich deren Sende- und Empfangsbereiche.
Gruß
Friemler
mal als Ansatz für Dein erstes Problem, die Lösung für das zweite (schwierigere) solltest Du daraus selbst ableiten können:
Die halbe Distanz zwischen zwei Punkten A und B mit den Koordinaten (Xa|Ya) und (Xb|Yb) lässt sich mit ein wenig Vektoralgebra berechnen. Sie entspricht dem halben Betrag des Richtungsvektors zwischen den Punkten A und B:
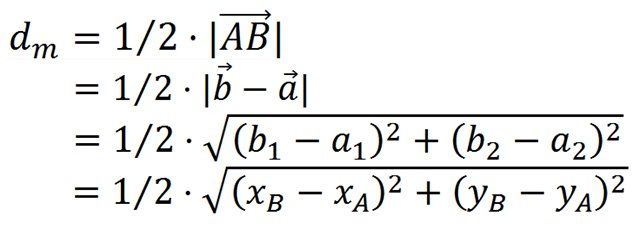
Die Koordinaten der halben Distanz lassen sich nach der Mittelpunktsformel berechnen:
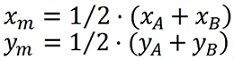
Wenn die halbe Distanz zwischen den WLAN Access Points A und B kleiner als die Reichweite beider Access Points ist, dann überschneiden sich deren Sende- und Empfangsbereiche.
Gruß
Friemler
