Sortieralgorithmus Mischsort

schnelle Datensortierung

Hallo zusammen! Bitsqueezer hat um eine Erklärung gebeten für den Sortieralgorithmus Mischsort: Hier ist sie:
Funktionsprinzip des Sortieralgorithmus Mischsort (Version 04-01-09):

Die zu sortierenden Daten stelle man sich als gemischtes Kartenspiel vor, zur Vereinfachung zunächst 32 Stück.
Im ersten Schritt werden diese Karten zu 16 geordneten 2-er Stapeln ausgelegt, jeweils die kleinere auf die größere. Dann werden nacheinander daraus 8: 4-er Stapel, dann 4: 8-er Stapel, 2: 16-er Stapel und am Ende 1: 32-Stapel zusammengemischt,also stets zwei nebeneinanderliegende Stapel zu einem vereinigt. Die Ordnung wird dadurch hergestellt, dass jeweils die kleinere Karte genommen wird, die auf einem der beiden Teilstapel oben liegt. Da diese aus dem vorangegangenen Schritt geordnet vorliegen, braucht dabei stets nur die oberste Karte betrachtet werden und nicht der ganze Stapel. Damit entfallen sehr viele If-Abfragen, was die Zeitersparnis gegenüber anderen Sortiermethoden wie z.B. „bubblesort" begründet.

In der Praxis der Datensortierung ergeben sich zwei -komlizierende- Unterschiede zum einfachen Bild von oben:
1.) Beim Karteneinsammeln nimmt man den neu entstehenden Stapel in die Hand, beim Datensortieren verbleibt er im Datenstapel: Das „Mischen" ist ein Verwalten von Nummern im Datenarray. Von den zwei zu mischenden „Teilstapeln" wird der „obere" in ein Hilfsarray kopiert, die alten Adressen sind zum Einsortieren der Daten frei. Wenn Daten vom „unteren Teilstapel" nach oben sortiert werden, machen sie unten weitere Plätze frei, sodass der freie Bereich stets genauso gross ist wie die Anzahl der einzusortierenden Daten.
2.) Die Datenarrays haben in der Praxis kaum je die Länge von glatten 2-er-Potenzen wie 4,8,16,32 usw. Daher geht das Zusammenmischen meist nicht glatt auf: Es bleiben „Reststapel" mit „krummen Stapelhöhen" übrig, die jeweils mitzuverwalten sind. Diese Reststapel spielen aber nur dann eine Rolle, wenn beim Durchlaufen der äußeren Programmschleife ein neu entstehender Reststapel (die Zahl der regulären Stapel war dann ungerade) auf einen schon von früher vorhandenen trifft: diese beiden Reststapel müssen dann zusammengemischt werden. Ist nur ein einzelner Reststapel vorhanden, so verbleibt er als „alter" Reststapel solange am Ende des Arrays, bis er auf einen „neuen" trifft, spätestens nach dem letzten Schleifendurchlauf, wenn das -fast- fertig gemischte Array diesen „neuen" Reststapel bildet.

Rechenzeitvergleich:
Den experimentellen Tests lag jeweils ein Datenarray aus ganzzahligen Zufallszahlen zugrunde, verglichen wurden Sortierzeiten für dieselben Arrays, für jede Feldlänge mehrfach, um statistische Ausreißer bei den Verteilungen zu minimieren.
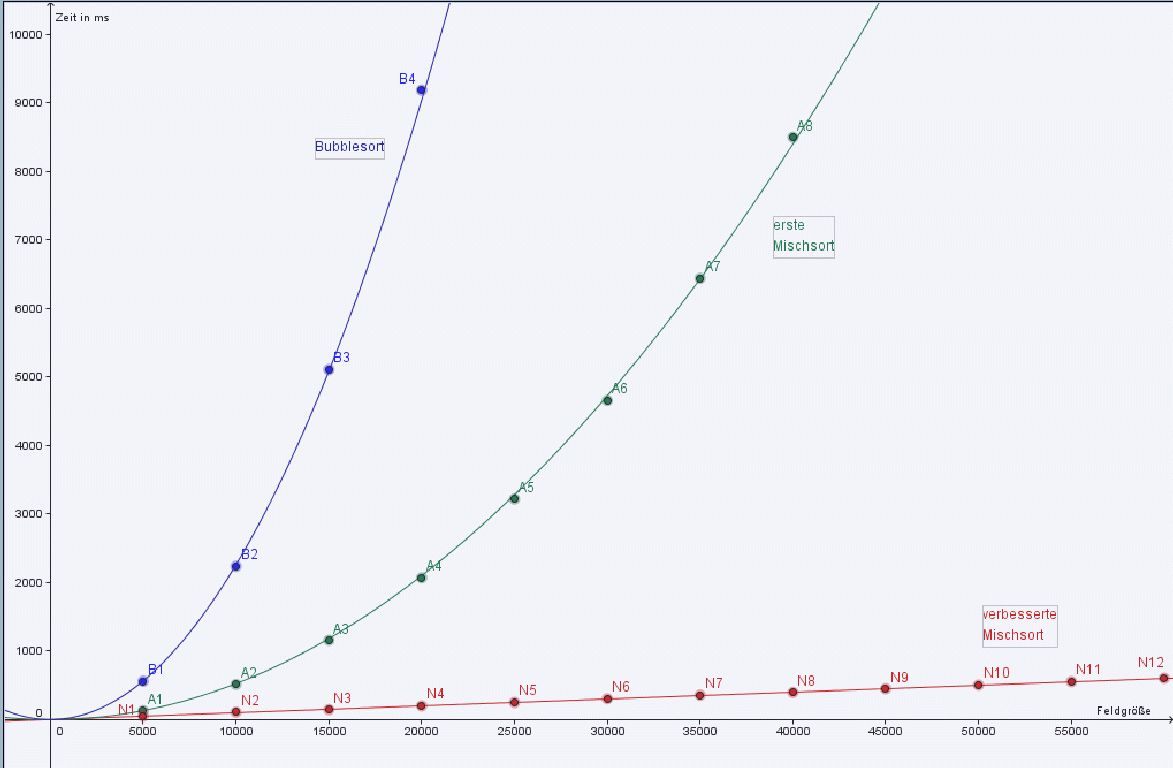
Bei der als „Bubblesort" bekannten Methode ist die Rechenzeit t = k*x(x-1) , wenn x die Anzahl der zu sortierenden Daten ist, dies ergibt sich aus der Zahl der zu durchlaufenden If- Abfragen und wurde gut bestätigt.
In einer vorangegangenen Version von Mischsort (dabei wurden die Teilstapel ohne einen Hilfsarray zusammensortiert, wozu vielfach Teilstapel verschoben wurden) ergab sich ein gleicher funktionaler Zusammenhang allerdings bei nur ca. 22% Zeitaufwand.
Durch Einführen des Hilfsarrays veränderte sich die Zeitabhängigkeit völlig: t ist direkt proportional zu x, was die Rechenzeit vor allem bei großen Datenmengen radikal verkürzt.

Graphische Auswertung:


Hier der Quelltext des Sortieralgorithmus, bestehend aus zwei Funktionen:
void Mixer(double dat1[65535],int ugos, int ugus,int hos, int hus)
/* ####################################################################### */
/* Sortierfunktion: mischt zwei geordnete Datenstapel zu einem neuen */
/* geordneten Datenstapel. */
/* enthält die einzige Sortieranweisung: zum Abwärtssortieren ist die */
/* Bedingung "dat1(ugus)<dat1(ugos)"in der einzigen if-Bedingung zu er- */
/* setzen durch "dat1(ugus)>dat1(ugos)" */
/* ####################################################################### */
{
double tv[32768]; int utvz = 1;
for(int i=1;i<=hos;i++){tv[i]=dat1[ugos+i-1];} /* kopiert den oberen Teilstapel */
while (hus*hos>0) /* Abbruch, wenn ein Teildatenstapel leer ist */
{
if(dat1[ugus]<tv[utvz])
{
dat1[ugos]=dat1[ugus]; /* oberes Element vom unteren Stapel einsortieren */
hus--;ugus++; /* Stapelhöhe- und -grenze (unt.Stapel)heraufsetzen */
}
else
{
dat1[ugos]=tv[utvz]; /* oberes Element vom Kopierstapel einsortieren */
hos--;utvz++; /* Stapelhöhe- und -grenze (Kop.Stapel)heraufsetzen */
}
ugos++;
}
while(hos>0) /* Reste vom oberen Stapel einkopieren */
{
dat1[ugos]=tv[utvz]; /* oberes Element vom Kopierstapel einsortieren */
hos--;utvz++;ugos++; /* Stapelhöhe- und -grenze (Kop.Stapel)heraufsetzen */
}

return;
}


void Mixsortierer(double dat1[65535],int ianz)

/* ####################################################################### */
/* Erstellt, verwaltet und zählt Datenstapel und */
/* übergibt sie an die eigentliche Sortierfunktion "Mixer". */
/* Übergibt das Datenfeld dat1 geordnet ans Hauptprogramm zurück. */
/* ####################################################################### */
{short zremi; int hst=1; int rstha=0; int rsthn; int stz=ianz; int ugost;
while (hst<ianz) /* zählt die Teilstapelhöhen */
{
rsthn=hst*(stz%2); /* prüft, ob ein neuer Reststapel entsteht */
zremi=0;if(0<rstha*rsthn){zremi=1;} /* prüft, ob ein alter und ein neuer Reststapel vorhanden ist */
ugost = 1;
while (ugost <1+ianz-hst-rsthn-rstha) /* verwaltet die Anfangsadresse des oberen Stapels */
{
Mixer(dat1,ugost,ugost+hst,hst,hst); /* übergibt die Anfangsadressen beider Stapel und die gemeinsame Stapelhöhe */
ugost+=(2*hst);
}
if(zremi == 1) /* wenn alter und neuer Reststapel vorhanden sind, werden diese gemischt */
{
Mixer(dat1,ugost,ugost+rsthn,rsthn,rstha); /* übergibt die Anfangsadressen beider Reststapel und die unterschiedlichen Stapelhöhen*/
}
rstha+=rsthn; /* Aktualisiert die Höhe des "alten" = jetzt einzigen Reststapels */
stz/=2;hst*=2; /* Aktualisiert Zahl und Höhe der normalen Stapel */
}
return;
}

so on, karhu612