SPC23 - 512-Bit Block Cipher Algorithm
Von Patrick Meyer und Sebastian Stein.
xor-base.dynu.net
SPC23 ist ein symmetrischer blockverschlüsselungs Algorithmus, der primär von mir, Patrick Meyer entwickelt wurde. Ein guter Freund aus Deutschland, Sebastian Stein möchte ich hier als Co. Autor erwähnen. Der Name SPC23 wurde aus unseren Namen abgeleitet, die Zahl 23 steht symbolisch.
SPC23 steht demnach für “SEBASTIAN PATRICK CIPHER 23”.
Der Cipher ist ein 16-Runden (8 cycles) Feistel-netzwerk mit einer Funktion F. Er arbeitet mit einer Blockgrösse von
128 Bit und Schlüsseln der Länge 512 Bit. Der Algorithmus besteht aus Schlüsselexpansion und Datenverschlüsselung.
Die Schlüsselexpansion wandelt einen Schlüssel von 512 Bit, in verschiedene Teilschlüssel um, die zusammen 1024 Bit umfassen. SPC23 verwendet acht vom Schlüssel abhängige S-Boxen, und ein dynamisches vom Schlüssel abhängiges
P-Array, das aus einem Teilresultat der Schlüsselexpansion berechnet wird.
Der Algorithmus ist nicht patentiert und darf von jedem frei implementiert und benutzt werden, sofern die Namen der Autoren, Patrick Meyer – Sebastian Stein vermerkt werden.

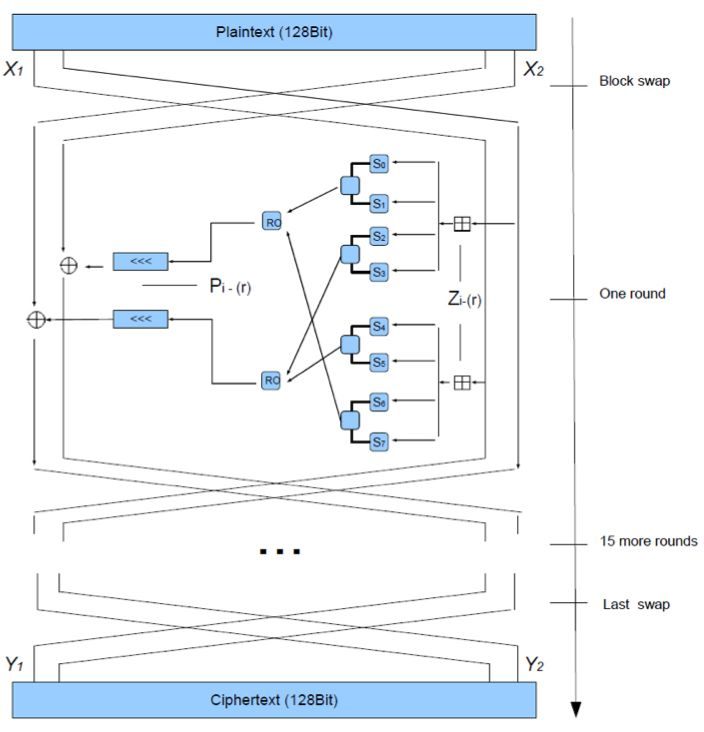
Die Datenverschlüsselung besteht aus einer Funktion die sechs-zehnmal durchlaufen wird. Jede Runde besteht aus einer Schlüssel und Daten abhängigen Permutation sowie einer Schlüssel und Daten abhängigen Substitution. Alle Operationen
sind Additionen und Xor-Verknüpfungen von 32 Bit Worten, dazu kommen 12 Tabellenindizierungen pro Runde. Dazu kommt eine rotierende Operator Funktion, genannt RO, die zwei 32Bit Worte berechnet aus Addition, Subtraktion
oder Xor-Verknüpfungen je nach Runde Modulo 4.
SPC23 besteht aus einem Feistel-Netzwerk mit 16 Runden.
Die Eingabe ist ein 128Bit langes Datenelement X. Die Verschlüsselung läuft wie folgt:
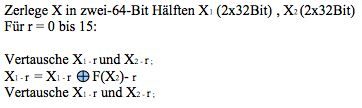
Die Entschlüsselung verläuft genau wie die Verschlüsselung, nur werden jetzt die Runden Schlüssel :
Z1,1, Z1,2,...,Z1,16 + Z2,1, Z2,2,...,Z2,16 ,
und das P-array :
P1,1, P1,2,...,P1,16 + P2,1, P2,2,...,P2,16
in umgekehrter Reihenfolge benutzt.
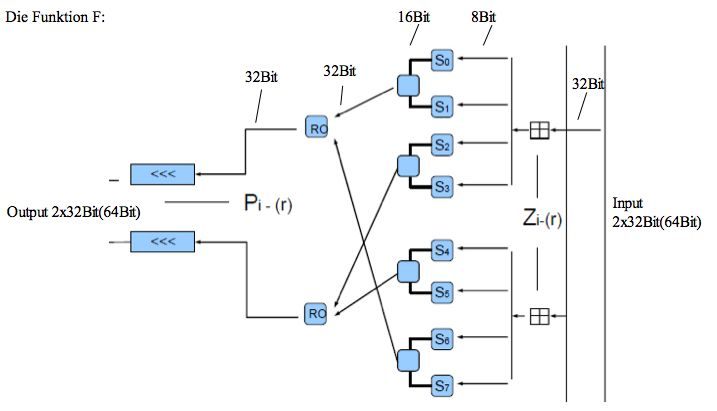
Die Funktion F sieht wie folgt aus:
Addiere den linken Block X1 (2x32Bit) mit dem Runden Schlüssel Z - r (2x32Bit). Zerlege den 2x32Bit Block X1 (linker Block) in acht 8Bit achtel a, b, c, d, e, f, g, h , die den Input für die S-Boxen bilden. Nach der Transformation in den 8*16 S-Boxen wird S0(16Bit) und S1(16Bit) zu 32Bit konkateniert, mit S2 bis S7 wird gleich verfahren. Jetzt haben wir vier konkatenierte 32Bit Blöcke, die den Input für die RO Funktion bilden. Nach SPC23 Standard bilden das erste konkatenierte paar (S0-S1) und das letzte (S6-S7) den Input für RO0, und das zweite (S2-S3) und dritte (S4-S5) den Input für RO1. Die Funktion RO ist ein rotierende Operator Funktion, das heisst das immer von der Runde (Mod 4) abhängig entweder Xor, Addition oder Subtraktion verwendet wird. Danach werden die 2x32Bit Blöcke einer Bit-weise shift Funktion unterzogen, dessen Key aus den letzten 5Bit der Runden permutations Bytes bestehen.
F(X2) = P(RO0( (S0(a(kav)), S1(b(kav)), (S6(g(kav),S7(h(kav)))) | P( RO1((S2(c(kav),S3(d(kav)),(S4 (e (kav),S5(f(kav))))
Anschliessend wird jetzt X2 (2x32Bit)(rechter Block) mit dem Output der Funktion F() Xor-t, um dann selbst zum rechten Block der nächsten Runde zu werden. Der linke Block X1 wird unmittelbar ohne mathematische Behandlung zum linken
Block der nächsten Runde.
SPC23 arbeitet mit einer grossen Zahl von Teilschlüsseln, die vor jeder Ver- oder Entschlüsselung im voraus berechnet werden müssen.
Der 64Byte bzw. 512Bit lange Hauptschlüssel (Masterkey) wird in 2 Blöcke der Grösse 2*256Bit bzw. 2*32Byte gespalten. Eine P-Box die 256Byte umfasst, (statisch fest im Algorithmus implementiere) wird jetzt Bit-weise mit dem ersten Block 32Byte(256Bit) des Hauptschlüssels permutiert. Mit dem zweiten Block 32Byte(256Bit) des Hauptschlüssels wird gleich verfahren, ausser das er mit einer zweiten (statisch fest im Algorithmus implementierten) P-Box an 256Byte, permutiert wird.
Der permutierte 64Byte(512Bit) Hauptschlüssel dient als Input für die Byte-weise shift Funktion der Schlüsselexpansion. Anschliessend wird der Hauptschlüssel Byte weise Xor-verknüpft mit einer dritten P-Box die 256Byte umfasst (statisch fest im Algorithmus implementierten) , was den Input für die Substitutions Funktion der Schlüsselexpansion ergibt. Die dritte P-Box wird jetzt in 64 Runden, einer Byte-weisen shift Funktion und anschliessend einer Substitutions Funktion der Schlüsselexpansion unterzogen. Danach wird die ganze Operation nochmal 64mal durchlaufen.
Mit der fertig berechneten dritten P-Box werden jetzt für jede der (Standard) 16 Runden von SPC23, einen 2*32Bit Teilschlüssel generiert. Die berechnete dritte P-Box wird ausserdem als Key-array für die Dynamisch zu erzeugenden S & P-Boxen des Algorithmus gespeichert.
Die 16 Runden Schlüssel sind je (2*32)64Bit lang.
Z1,1, Z1,2,...,Z1,16
Z2,1, Z2,2,...,Z2,16
Die Funktion zum erzeugen des dynamischen P-array, hat eine 128Byte grosse P-Box der Grösse 8Bit (statisch fest im Algorithmus implementiere) . Die Finale P-Box der Schlüsselexpansion wird als Key-array benützt. Die ersten 128byte werden der Byte-weisen shift Permutations Funktion zugeteilt die anderen 128byte der Substitutions Funktion. Zuerst wird die P-Box initialisiert .Danach werden die 2 Funktionen 128 mal nacheinander auf die P-Box angewendet. Wie schon erwähnt bestehen die Funktionen zum einen aus einer Byte-weisen shift Permutation und zum anderen aus einer Substitution, die abhängig vom Wert mit einer anderen Position Substituert. Danach werden die P-Boxen (Permutationsschlüsseln) erzeugt. Da der Standard 16 Runden vorsieht werden jetzt aus der fertig berechneten P-Box die 128byte umfasst, 16 *(2*8)Bit Values erzeugt von denen immer nur die ersten 5Bit, für die dynamische shift Permutation des Algorithmus verwendet wird.
Das P-array besteht aus 16 Teilschlüsseln der Länge (2*8)16 Bit.
P1,1, P1,2,...,P1,16
P2,1, P2,2,...,P2,16
Die Funktion zur Erzeugung der dynamischen S-Boxen verläuft fast gleich wie bei der Erzeugung des dynamischen Parray. Ausser einer fest im Algorithmus implementierte S-Box die 256 Werte umfasst, die Values der Grösse 16Bit aufweist..
Zuerst wird die S-Box initialisiert, danach wie bei den P-Boxen eine shift und Substitutions Funktion die 128mal durchlaufen wird. Damit ist die erste S-Box berechnet. Diese Operationen werden jetzt 7 mal nacheinander ausgeführt, dazwischen werden die Zwischenergebnisse der S-Boxen immer mit der letzten S-box Xor-t, und als nächste zu Permutierende S-Box initialisiert. Die Substitutions Funktion des SPC23 Algorithmus ist die einzige nichtlineare Funktion.
8 S-Boxen der Grösse 8*16, 8Bit Input 16Bit Output. Die S-Boxen enthalten je 256 Einträge.
S1,0 ,S1,1 ,....., S1,255
S2,0 ,S2,1 ,....., S2,255
S3,0 ,S3,1 ,....., S3,255
S4,0 ,S4,1 ,....., S4,255
S5,0 ,S5,1 ,....., S5,255
S6,0 ,S6,1 ,....., S6,255
S7,0 ,S7,1 ,....., S7,255
S8,0 ,S8,1 ,....., S8,255
Die Performance wurde mit einem MS:VC++ 08 Compiler und einem CPU, Typ: Intel Core 2 Duo P8700 gemessen. Die Implementierung des Cipher wurde speziel für 32Bit Systeme optimiert. Der Quellcode wurde mit den folgenden Compiler spezifischen Optimierungen übersetzt.
MS VC++ 08 erzeugt 89 ASM Instruktionen pro Runde für den SPC23 Algorithmus. Die Instruktionen wurden anhand des disassemblierten Maschinencode ermittelt. Da der Cipher sehr schnell ist gegenüber DES und anderen Algorithmen ist er bestens für Echtzeitanwendungen geeignet. Die nachfolgende Tabelle enthält Performance vergleiche zu anderen bekannten Algorithmen, wie Twofish.
Plaintextsize : 128Bit
Keysize : 512Bit
Klartext : 0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30
Schlüssel : 0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,
0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,
0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,
0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30
Ciphertext : 0xa4 ,0x37 ,0x7b ,0x10 ,0x0b ,0x5a ,0x1e ,0xf0 ,0x5e ,0x77 ,0x70 ,0x2a ,0x79 ,0xf9 ,0xfd ,0xe1
Quellcode:
SPC23_LIB.c
SPC23_LIB.h
test_SPC23_Cipher.c
PDF:
SPC23_paper.pdf
SPC23_schema.pdf
xor-base.dynu.net
Inhaltsverzeichnis
SPC23 steht demnach für “SEBASTIAN PATRICK CIPHER 23”.
Der Cipher ist ein 16-Runden (8 cycles) Feistel-netzwerk mit einer Funktion F. Er arbeitet mit einer Blockgrösse von
128 Bit und Schlüsseln der Länge 512 Bit. Der Algorithmus besteht aus Schlüsselexpansion und Datenverschlüsselung.
Die Schlüsselexpansion wandelt einen Schlüssel von 512 Bit, in verschiedene Teilschlüssel um, die zusammen 1024 Bit umfassen. SPC23 verwendet acht vom Schlüssel abhängige S-Boxen, und ein dynamisches vom Schlüssel abhängiges
P-Array, das aus einem Teilresultat der Schlüsselexpansion berechnet wird.
Der Algorithmus ist nicht patentiert und darf von jedem frei implementiert und benutzt werden, sofern die Namen der Autoren, Patrick Meyer – Sebastian Stein vermerkt werden.


Die Datenverschlüsselung besteht aus einer Funktion die sechs-zehnmal durchlaufen wird. Jede Runde besteht aus einer Schlüssel und Daten abhängigen Permutation sowie einer Schlüssel und Daten abhängigen Substitution. Alle Operationen
sind Additionen und Xor-Verknüpfungen von 32 Bit Worten, dazu kommen 12 Tabellenindizierungen pro Runde. Dazu kommt eine rotierende Operator Funktion, genannt RO, die zwei 32Bit Worte berechnet aus Addition, Subtraktion
oder Xor-Verknüpfungen je nach Runde Modulo 4.
SPC23 besteht aus einem Feistel-Netzwerk mit 16 Runden.
Die Eingabe ist ein 128Bit langes Datenelement X. Die Verschlüsselung läuft wie folgt:
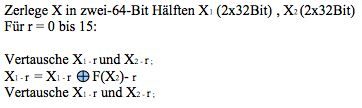
Die Entschlüsselung verläuft genau wie die Verschlüsselung, nur werden jetzt die Runden Schlüssel :
Z1,1, Z1,2,...,Z1,16 + Z2,1, Z2,2,...,Z2,16 ,
und das P-array :
P1,1, P1,2,...,P1,16 + P2,1, P2,2,...,P2,16
in umgekehrter Reihenfolge benutzt.
Die Funktion F sieht wie folgt aus:
Addiere den linken Block X1 (2x32Bit) mit dem Runden Schlüssel Z - r (2x32Bit). Zerlege den 2x32Bit Block X1 (linker Block) in acht 8Bit achtel a, b, c, d, e, f, g, h , die den Input für die S-Boxen bilden. Nach der Transformation in den 8*16 S-Boxen wird S0(16Bit) und S1(16Bit) zu 32Bit konkateniert, mit S2 bis S7 wird gleich verfahren. Jetzt haben wir vier konkatenierte 32Bit Blöcke, die den Input für die RO Funktion bilden. Nach SPC23 Standard bilden das erste konkatenierte paar (S0-S1) und das letzte (S6-S7) den Input für RO0, und das zweite (S2-S3) und dritte (S4-S5) den Input für RO1. Die Funktion RO ist ein rotierende Operator Funktion, das heisst das immer von der Runde (Mod 4) abhängig entweder Xor, Addition oder Subtraktion verwendet wird. Danach werden die 2x32Bit Blöcke einer Bit-weise shift Funktion unterzogen, dessen Key aus den letzten 5Bit der Runden permutations Bytes bestehen.
F(X2) = P(RO0( (S0(a(kav)), S1(b(kav)), (S6(g(kav),S7(h(kav)))) | P( RO1((S2(c(kav),S3(d(kav)),(S4 (e (kav),S5(f(kav))))
Anschliessend wird jetzt X2 (2x32Bit)(rechter Block) mit dem Output der Funktion F() Xor-t, um dann selbst zum rechten Block der nächsten Runde zu werden. Der linke Block X1 wird unmittelbar ohne mathematische Behandlung zum linken
Block der nächsten Runde.

SPC23 arbeitet mit einer grossen Zahl von Teilschlüsseln, die vor jeder Ver- oder Entschlüsselung im voraus berechnet werden müssen.
Der 64Byte bzw. 512Bit lange Hauptschlüssel (Masterkey) wird in 2 Blöcke der Grösse 2*256Bit bzw. 2*32Byte gespalten. Eine P-Box die 256Byte umfasst, (statisch fest im Algorithmus implementiere) wird jetzt Bit-weise mit dem ersten Block 32Byte(256Bit) des Hauptschlüssels permutiert. Mit dem zweiten Block 32Byte(256Bit) des Hauptschlüssels wird gleich verfahren, ausser das er mit einer zweiten (statisch fest im Algorithmus implementierten) P-Box an 256Byte, permutiert wird.
Der permutierte 64Byte(512Bit) Hauptschlüssel dient als Input für die Byte-weise shift Funktion der Schlüsselexpansion. Anschliessend wird der Hauptschlüssel Byte weise Xor-verknüpft mit einer dritten P-Box die 256Byte umfasst (statisch fest im Algorithmus implementierten) , was den Input für die Substitutions Funktion der Schlüsselexpansion ergibt. Die dritte P-Box wird jetzt in 64 Runden, einer Byte-weisen shift Funktion und anschliessend einer Substitutions Funktion der Schlüsselexpansion unterzogen. Danach wird die ganze Operation nochmal 64mal durchlaufen.
FOR(X=0; X < 64 ;X++) {
FOR(I=0; I < 64 ;I++) {
SHIFT();
(SUBKEY % 2) == 0 ? SUB0() : SUB1() ;
}
}Mit der fertig berechneten dritten P-Box werden jetzt für jede der (Standard) 16 Runden von SPC23, einen 2*32Bit Teilschlüssel generiert. Die berechnete dritte P-Box wird ausserdem als Key-array für die Dynamisch zu erzeugenden S & P-Boxen des Algorithmus gespeichert.
Die 16 Runden Schlüssel sind je (2*32)64Bit lang.
Z1,1, Z1,2,...,Z1,16
Z2,1, Z2,2,...,Z2,16
Die Funktion zum erzeugen des dynamischen P-array, hat eine 128Byte grosse P-Box der Grösse 8Bit (statisch fest im Algorithmus implementiere) . Die Finale P-Box der Schlüsselexpansion wird als Key-array benützt. Die ersten 128byte werden der Byte-weisen shift Permutations Funktion zugeteilt die anderen 128byte der Substitutions Funktion. Zuerst wird die P-Box initialisiert .Danach werden die 2 Funktionen 128 mal nacheinander auf die P-Box angewendet. Wie schon erwähnt bestehen die Funktionen zum einen aus einer Byte-weisen shift Permutation und zum anderen aus einer Substitution, die abhängig vom Wert mit einer anderen Position Substituert. Danach werden die P-Boxen (Permutationsschlüsseln) erzeugt. Da der Standard 16 Runden vorsieht werden jetzt aus der fertig berechneten P-Box die 128byte umfasst, 16 *(2*8)Bit Values erzeugt von denen immer nur die ersten 5Bit, für die dynamische shift Permutation des Algorithmus verwendet wird.
Das P-array besteht aus 16 Teilschlüsseln der Länge (2*8)16 Bit.
P1,1, P1,2,...,P1,16
P2,1, P2,2,...,P2,16
Die Funktion zur Erzeugung der dynamischen S-Boxen verläuft fast gleich wie bei der Erzeugung des dynamischen Parray. Ausser einer fest im Algorithmus implementierte S-Box die 256 Werte umfasst, die Values der Grösse 16Bit aufweist..
Zuerst wird die S-Box initialisiert, danach wie bei den P-Boxen eine shift und Substitutions Funktion die 128mal durchlaufen wird. Damit ist die erste S-Box berechnet. Diese Operationen werden jetzt 7 mal nacheinander ausgeführt, dazwischen werden die Zwischenergebnisse der S-Boxen immer mit der letzten S-box Xor-t, und als nächste zu Permutierende S-Box initialisiert. Die Substitutions Funktion des SPC23 Algorithmus ist die einzige nichtlineare Funktion.
8 S-Boxen der Grösse 8*16, 8Bit Input 16Bit Output. Die S-Boxen enthalten je 256 Einträge.
S1,0 ,S1,1 ,....., S1,255
S2,0 ,S2,1 ,....., S2,255
S3,0 ,S3,1 ,....., S3,255
S4,0 ,S4,1 ,....., S4,255
S5,0 ,S5,1 ,....., S5,255
S6,0 ,S6,1 ,....., S6,255
S7,0 ,S7,1 ,....., S7,255
S8,0 ,S8,1 ,....., S8,255
Die Performance wurde mit einem MS:VC++ 08 Compiler und einem CPU, Typ: Intel Core 2 Duo P8700 gemessen. Die Implementierung des Cipher wurde speziel für 32Bit Systeme optimiert. Der Quellcode wurde mit den folgenden Compiler spezifischen Optimierungen übersetzt.
- Full Optimization /Ox
- Inline Function Expansion /Ob2
- Intrinsic Function /Oi
- Favor Fast Code /Ot
MS VC++ 08 erzeugt 89 ASM Instruktionen pro Runde für den SPC23 Algorithmus. Die Instruktionen wurden anhand des disassemblierten Maschinencode ermittelt. Da der Cipher sehr schnell ist gegenüber DES und anderen Algorithmen ist er bestens für Echtzeitanwendungen geeignet. Die nachfolgende Tabelle enthält Performance vergleiche zu anderen bekannten Algorithmen, wie Twofish.
| Algorithmus | Encryption | Decryption | Mean |
|---|---|---|---|
| AES | 94.8 MB/s | 94.2 MB/s | 94.5 MB/s |
| SPC23 | 88,1 MB/s | 86,2 MB/s | 87.1 MB/s |
| Twofish | 81.7 MB/s | 85.9 MB/s | 83.8 MB/s |
| Serpent | 42.1 MB/s | 43.8 MB/s | 42.9 MB/s |
Plaintextsize : 128Bit
Keysize : 512Bit
Klartext : 0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30
Schlüssel : 0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,
0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,
0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,
0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30 ,0x30
Ciphertext : 0xa4 ,0x37 ,0x7b ,0x10 ,0x0b ,0x5a ,0x1e ,0xf0 ,0x5e ,0x77 ,0x70 ,0x2a ,0x79 ,0xf9 ,0xfd ,0xe1
Quellcode:
SPC23_LIB.c
SPC23_LIB.h
test_SPC23_Cipher.c
PDF:
SPC23_paper.pdf
SPC23_schema.pdf
Bitte markiere auch die Kommentare, die zur Lösung des Beitrags beigetragen haben
Content-ID: 143483
Url: https://administrator.de/tutorial/spc23-512-bit-block-cipher-algorithm-143483.html
Ausgedruckt am: 23.07.2025 um 10:07 Uhr